

Each axis, x, is crossing the centroid and parallel to the base of the area. 10.5 Sections rotating and participating in bending of the beams denoted as case 1 and 2. Presentation and proof of equations regarding bending stiffness is out of scope of this course. For this cross section, the moment of inertia of its section (perpendicular to the beam axis) is about the axis crossing the centroid of the section see Fig. The bending stiffness is directly related to the moment of inertia of the beam’s cross section as shown in Fig. 10.4 Two cases of bending of beams under the same load. This structural behavior is explained by the bending stiffness of the beam. If the deformation is measured by the beam deflection,, at its half length, we can observe that and. Under the same load, it is tangible that the bending beam deforms less in case 1 than in case 2. In case one, the beam is placed flat on the supports while it is vertically positioned in the second case. As an example consider bending of a lumber beam loaded by a single force as shown in Fig. In addition to other factors like the material and length of a beam, the bending stiffness directly depends on the moment of inertia of the beam cross section(s) perpendicular to the longitudinal axis of the beam. The deformation of a beam under bending is directly related to its bending stiffness. A physical application of the moment of inertia of an area: bending stiffness You will observe that for a circular area. You should consider a differential strip as shown below. Where is a differential element of area (in the Cartesian coordinate system) as shown in Fig. 10.2 can generally be evaluated using double integrals in a Cartesian coordinate system as, Where and are squared distances from the differential area (infinitesimal in all directions) to the x and y axes respectively (i.e., the coordinates of the differential area). 10.2), the moments of inertia of an area about the x and y axes are denoted as and and determined by, If x and y are two perpendicular axes (Fig. The moment of inertia, or more accurately, the second moment of area, is defined as the integral over the area of a 2D shape, of the squared distance from an axis: I\iintA y2 dA where A is the area of the shape and y the distance of any point inside area A from a given axis of rotation. When the moment of inertia is calculated about two orthogonal axes in the plane of the area, it is called the rectangular moment of inertia. The word moment is used because terms like meaning distance to an axis multiplied by an area are analogous to the definition of the moment of a force expressing distance to an axis multiplied by a force. The centroid of an area,, is called the first moment of area. The moment of inertia is also called the second moment of area. 10.1 Terms involved in calculating the moment of inertia of an area about an axis m.
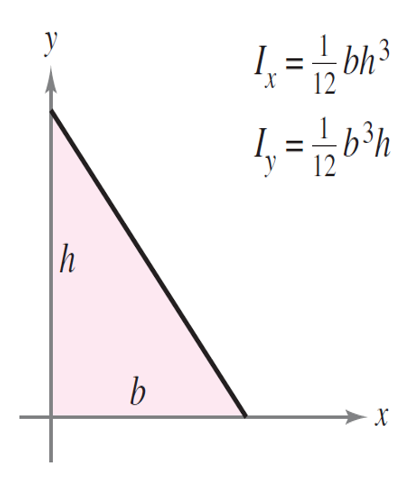
This quantity has the dimension of the length to the power of four (e.g. The value of depends on the location and direction of the axis, and the shape of the area. The differential element,, in this definition, is infinitesimal (approaching to zero) in any directions on the plane. Where is the moment of inertia of the area about an axis in the plane of the area, and is the perpendicular distance from the axis m to the differential area as shown in Fig. The mathematical definition of the moment of inertial of an area (two-dimensional region) about an axis is, stiffness) is against bending or twisting about some axis. Its value reflects how strong an object (i.e. The moment of inertia of an area is a geometric property of the area. The moment of inertia of an area about an axis is a concept appearing in the formulations of several physical phenomena. Open Educational Resources Moments of Inertia of area: Relationships between Load, Shear, and Moments.Shear and moment equations and their diagrams.Conditions for two dimensional rigid-body equilibrium.Equilibrium of Particles and Rigid Bodies.




 0 kommentar(er)
0 kommentar(er)
